


Die Aufrufsyntax des Programmes druck lautet
druck (ski, Fz, My, Mx, d);
ski ist der Name der Skibeschreibungsdatei, Fz, My, Mx
geben die durch den Skifahrer aufgebrachten Kräfte und Momente und
d ist ein Maß für die Schneehärte.
Die Zeichenkette ski gibt den Namen der Skibeschreibungsdatei an. Die Default-Erweiterung '.dat' wird, falls notwendig, automatisch angehängt. Diese Datei muss sich im aktuellen Arbeitsverzeichnis des Matlab-Programmes befinden oder durch einen vollständigen Pfad angegeben werden. Das Format dieser Datei wird im folgenden Unterkapitel beschrieben.
Fz, My und Mx geben die Belastung durch den Skifahrer an und werden als Punktlast im Bindungsmontagepunkt aufgebracht.
Es ist Fz die Normalkraft auf den Ski in [N]. Sie ist von der Größenordnung . Hierin sind die Masse des Skifahrers samt Ausrüstung, der Betrag der Geschwindigkeit, der Schwungradius, die Schwerebeschleunigung und der Kantwinkel.
Das Vorlage/Rücklagemoment My ist das Moment um die Skibreitenachse und wird in [Nm] angegeben. Es ist positiv bei Vorlage und negativ bei Rücklage.
Das Kantmoment Mx ist dafür verantwortlich, dass der Ski aufgekantet wird. Es ist positiv oder negativ, je nachdem ob der Ski nach links oder rechts aufgekantet wird. Die Einheit für das Kantmoment ist [Nm].
Wir nehmen an, dass der Ski symmetrisch bezüglich der Breitenachse aufgebaut ist. Daher genügt es, die Berechnungen für positive Aufkantmomente durchzuführen. Um die Ergebnisse bei der Darstellung besser skalieren zu können, lassen wir nur positive Werte von Mx zu.
Die Schneehärte wird durch den Parameter d gesteuert. d gibt die Eindringtiefe eines starren Brettes mit einer Länge von 1.5 m und einer Breite von 0.07 m, wenn es mit einer Kraft von 1000 N senkrecht auf die Schneeoberfläche gedrückt wird. Der Wert von d wird in [m] angegeben.
d ist ein optionaler Parameter. Als Default-Wert wird 0.001 m verwendet. Dies entspricht eher harten Verhältnissen.
Bei der Durchführung des Befehles druck werden mehrere Dateien mit der Bezeichnung tmp* erzeugt. Diese Dateien enthalten Zwischenergebnisse, welche die Eigenschaften und die Durchbiegung des Ski betreffen. Diese temporären Dateien werden zur Darstellung der Druckverteilung verwendet. Bei jedem Aufruf von druck werden diese Dateien überschrieben.
Da die Berechnung der Druckverteilung rechenintensiv ist, wurde ein m-File geschrieben, welcher das jeweils letzte Berechnungsergebnis darstellt. Es wird durch den Befehl edgbed; aufgerufen.
Die Online-Dokumentation wird mit dem Befehl druckdoc; aufgerufen.
Die Skibeschreibungsdatei beschreibt den Aufbau von Skiern. Diese Datei wird von uns auch für andere Berechnungen verwendet, sodass sie auch Daten enthält, welche zwar für das vorliegende Programm redundant sind, aber dennoch mit sinnvollen Werten belegt werden müssen.
Nachfolgend geben wir den Aufbau der Skibeschreibungsdatei an. Sinnvollerweise wird man für einen neuen Ski dieses Beispiel kopieren und modifizieren.
Die Datei beginnt mit einem Header von 12 Zeilen.
! ! Ski: Head Cyber Race 23/190 ! ! Messung: M. Moessner ! Datum: 1998-10-01 ! ! Folgende Daten wurden an einem Head Cyber Race ohne montierter ! Bindung und ohne Bindungsplatte aufgenommen. ! ! ! !Der Header wird vom Programm überlesen. Der Benutzer kann dort Informationen zur Messung der Daten ablegen. Es folgt ein Block mit den Kenndaten des verwendeten Ski.
2 ! data flag 1.870 ! L projected length 1.690 ! L_c contact length, L_f + l_b 0.790 ! L_mp position of mounting point 0.790 ! L_p midpoint between mounted bindings 0.950 ! L_f contact length of afterbody 0.740 ! L_b contact length of forebody 22.4 ! ski radius r_s 1.76 ! ski mass m 0.945 ! center of mass position x_s 0.0022 ! 0.00124 m inertia moment I_xx 0.453 ! 0.257 m inertia moment I_yy 0.468 ! 0.266 m inertia moment I_zz 0.0 ! inertia moment I_xy 0.0 ! inertia moment I_xz 0.0 ! inertia moment I_yz
Das Flag flag gibt an, ob der Ski als geschichteter Balken modelliert wird (flag=1) oder ob alle Größen durch Messdaten gegeben sind (flag=2). Die vorliegende Version des Programmes ist für die Situation flag=2 vorgesehen.
Bei den nachfolgenden Bezeichnungen beziehen wir uns auf die Begriffsdefinitionen durch ISO 6289 bzw. ÖNORM S 4020. Es ist die projizierte Skilänge, die Kontaktlänge, die Position des Bindungsmontagepunktes und die Position des Mittelpunktes zwischen beiden montierten Bindungsteilen. Oft wird die Bindung so montiert, dass gilt. Die Kontaktlänge teilt sich in einen Teil vor dem Mittelpunkt der beiden Bindungsbacken und einen Teil dahinter auf. Die entsprechenden Längen sind und . ist der Krümmungsradius des Seitenformausschnittes, welcher oft auch als Skiradius bezeichnet wird. ist die Masse des Ski, die longitudinale Position des Schwerpunktes und die Komponenten des Trägheitstensors.
Im nächsten Abschnitt wird der Skiaufbau beschrieben. Wir behandeln diesen Block nicht näher, da diese Daten bei flag=2 zwar eingelesen, aber zur Berechnung der Druckverteilung nicht verwendet werden. Dennoch ist es aus programmtechnischen Gründen notwendig, sinnvolle Werte anzugeben.
Will man mit variablem Skiaufbau experimentieren, so kann man flag=1 setzen und die nachfolgenden Konstanten variieren.
! ! constants for sophisticated usage ! 7 ! spline degree 0.004 ! wb, ski upper part 2*wb smaller than edges 0.0017 ! dt, thickness of top surface 0.36 ! dt1, fraction of 1st layer in dt 0.36 ! dt2, fraction of 2nd layer in dt 0.28 ! dt3, fraction of 3ed layer in dt 0.0 ! dt4, fraction of 4th layer in dt 0.0 ! dt5, fraction of 5th layer in dt 0.40 ! h1, fraction of upper component 0.000 ! di, thickness of steel-insert 1.000 ! fi, forward end of steel-insert -1.000 ! bi, backward end of steel-insert 1.000 ! si, length of slope of steel-insert 0.00 ! h3, fraction of middle component 0.003 ! db, thickness of binding-insert 0.600 ! fb, forward end of binding-insert 0.000 ! bb, backward end of binding-insert 0.400 ! sb, slope of binding-insert 0.60 ! h5, fraction of lower component 0.00195 ! db, thickness of running surface 0.0 ! db1, fraction of 1st layer in db 0.0 ! db2, fraction of 2nd layer in db 0.185 ! db3, fraction of 3ed layer in db 0.215 ! db4, fraction of 4th layer in db 0.6 ! db5, fraction of 5th layer in db 0.002 ! sw, width of side wall 0.00195 ! eh1, edge height 1 0.0022 ! ew1, edge width 1 0.00 ! eh2, edge height 2 0.00 ! ew2, edge width 2 ! ! materials ! 71 31 83 1 1 ! upper part, from top to bottom 78 1 1 81 78 ! kernel, from top to bottom 1 1 83 31 75 ! lower part, from top to bottom 81 5 ! side wall, edge
Als letzter Datenblock folgt die Beschreibung der Skigeometrie und die Angabe der Materialeigenschaften. Er beginnt mit einem 15 Zeilen langen Kommentarteil. Es folgen die Anzahl der Messpunkte n, 3 Kommentarzeilen, die Standardabweichungen des Messfehlers von w, c, d, rho, EI und GJ, eine weitere Kommentarzeile und für jeden Messpunkt einen Zeile mit dem Messwert von s, w, c, d, rho, EI und GJ. Hierin sind s der Abstand des Messpunktes vom hinteren Skiende in [m], w die Skibreite in [m], c die Bogenhöhe in [m], d die Skidicke in [m], rho die Massen-Liniendichte in [kg/m], EI die Biegesteifigkeit in [] und GJ die Torsionssteifigkeit in [].
Die angegebenen Daten werden durch glättende Splines nach einem Verfahren von P. Dierckx dargestellt. Der Glättungsparameter der Spline-Approximation wird so gewählt, dass die Standardabweichung des Approximationsfehlers kleiner gleich dem vom Benutzer vorgegebenen Messfehler ist.
!
! s position coordinate, 0 at tail, L at tip
! w ski width
! t position of top surface, t = c + d
! d ski thickness
! c ski camber
!
! for flag = 2 additionally
!
! rho line-density
! EI bending stiffness
! GJ torsional stiffness
!
! s w c d rho EI GJ
!
108
!
! standard deviations of error in measurement of w, c, d, rho, EI, GJ
!
1.0e-4 1.0e-4 1.0e-4 1.0e-4 1.0e-2 1.0e-2
!
0.0000 0.0295 0.0070 0.0060 0.5014 27.83 34.81
0.0100 0.0354 0.0044 0.0061 0.5907 32.34 41.74
0.0200 0.0378 0.0027 0.0063 0.6594 36.80 47.71
0.0300 0.0414 0.0015 0.0065 0.7114 41.12 52.58
0.0400 0.0433 0.0001 0.0067 0.7505 45.27 56.61
0.0500 0.0447 0.0000 0.0069 0.7789 49.20 59.93
0.0600 0.0450 0.0000 0.0071 0.7989 52.86 62.64
0.0800 0.0447 0.0000 0.0072 0.8209 59.38 66.51
0.1000 0.0439 0.0000 0.0073 0.8282 64.90 68.92
0.1200 0.0432 0.0000 0.0074 0.8281 69.74 70.53
0.1400 0.0425 0.0000 0.0077 0.8253 74.33 71.84
0.1600 0.0420 0.0005 0.0080 0.8225 79.13 73.16
0.1800 0.0413 0.0011 0.0083 0.8211 84.57 74.72
0.2000 0.0406 0.0017 0.0086 0.8217 90.97 76.64
0.2200 0.0401 0.0024 0.0089 0.8243 98.56 78.97
0.2400 0.0394 0.0030 0.0092 0.8291 107.49 81.73
0.2600 0.0389 0.0035 0.0095 0.8357 117.80 84.91
0.2800 0.0384 0.0039 0.0099 0.8439 129.49 88.47
0.3000 0.0379 0.0046 0.0103 0.8534 142.50 92.37
0.3200 0.0374 0.0050 0.0107 0.8637 156.75 96.55
0.3400 0.0370 0.0055 0.0112 0.8745 172.10 100.92
0.3600 0.0365 0.0060 0.0117 0.8854 188.39 105.40
0.3800 0.0360 0.0065 0.0121 0.8964 205.43 109.95
0.4000 0.0356 0.0067 0.0125 0.9078 223.04 114.94
0.4200 0.0352 0.0070 0.0129 0.9197 240.99 121.11
0.4400 0.0348 0.0071 0.0133 0.9323 259.08 129.07
0.4600 0.0344 0.0073 0.0137 0.9456 277.10 138.79
0.4800 0.0341 0.0077 0.0140 0.9593 294.86 150.07
0.5000 0.0338 0.0079 0.0144 0.9731 312.22 162.77
0.5200 0.0334 0.0080 0.0148 0.9868 329.02 176.74
0.5400 0.0331 0.0082 0.0152 1.0000 345.17 191.80
0.5600 0.0328 0.0083 0.0155 1.0127 360.58 207.70
0.5800 0.0325 0.0085 0.0158 1.0247 375.18 224.16
0.6000 0.0323 0.0086 0.0161 1.0361 388.93 240.83
0.6200 0.0321 0.0086 0.0164 1.0467 401.78 257.41
0.6400 0.0319 0.0087 0.0167 1.0565 413.69 273.58
0.6600 0.0316 0.0088 0.0169 1.0655 424.64 289.04
0.6800 0.0314 0.0089 0.0171 1.0735 434.61 303.46
0.7000 0.0312 0.0091 0.0172 1.0804 443.57 316.51
0.7200 0.0312 0.0093 0.0173 1.0861 451.53 327.85
0.7300 0.0311 0.0094 0.0174 1.0884 455.13 332.78
0.7400 0.0310 0.0095 0.0174 1.0904 458.47 337.18
0.7600 0.0309 0.0097 0.0175 1.0934 464.41 344.23
0.7800 0.0308 0.0099 0.0176 1.0951 469.36 348.64
0.8000 0.0307 0.0099 0.0177 1.0960 473.33 350.54
0.8200 0.0307 0.0099 0.0177 1.0962 476.34 351.68
0.8400 0.0307 0.0099 0.0177 1.0962 478.39 352.53
0.8500 0.0307 0.0098 0.0177 1.0963 479.06 352.80
0.8600 0.0307 0.0099 0.0177 1.0963 479.49 352.98
0.8800 0.0306 0.0100 0.0177 1.0964 479.65 353.06
0.9000 0.0307 0.0101 0.0177 1.0966 478.86 352.81
0.9200 0.0307 0.0103 0.0177 1.0967 477.10 352.19
0.9400 0.0307 0.0102 0.0176 1.0967 474.36 351.15
0.9600 0.0307 0.0095 0.0176 1.0965 470.62 349.68
0.9800 0.0308 0.0097 0.0175 1.0962 465.86 347.77
1.0000 0.0309 0.0095 0.0174 1.0956 460.07 345.39
1.0200 0.0311 0.0094 0.0173 1.0948 453.21 342.55
1.0400 0.0312 0.0093 0.0172 1.0937 445.29 339.20
1.0600 0.0314 0.0092 0.0171 1.0923 436.30 335.34
1.0800 0.0316 0.0090 0.0169 1.0905 426.23 330.93
1.1000 0.0316 0.0089 0.0167 1.0884 415.12 325.95
1.1200 0.0319 0.0087 0.0165 1.0858 402.99 320.39
1.1400 0.0322 0.0084 0.0162 1.0828 389.87 314.24
1.1600 0.0324 0.0083 0.0159 1.0793 375.84 307.52
1.1800 0.0326 0.0081 0.0156 1.0752 360.95 300.24
1.2000 0.0330 0.0080 0.0152 1.0706 345.31 292.44
1.2200 0.0333 0.0078 0.0147 1.0655 329.01 284.13
1.2400 0.0336 0.0077 0.0143 1.0598 312.16 275.35
1.2600 0.0340 0.0075 0.0139 1.0536 294.89 266.09
1.2800 0.0343 0.0074 0.0135 1.0469 277.34 256.40
1.3000 0.0347 0.0072 0.0131 1.0398 259.65 246.33
1.3200 0.0350 0.0070 0.0128 1.0322 241.94 236.02
1.3400 0.0355 0.0069 0.0124 1.0243 224.38 225.62
1.3600 0.0359 0.0067 0.0120 1.0161 207.09 215.19
1.3800 0.0363 0.0066 0.0116 1.0076 190.21 204.61
1.4000 0.0367 0.0064 0.0112 0.9985 173.87 193.65
1.4200 0.0373 0.0063 0.0107 0.9881 158.18 182.13
1.4400 0.0377 0.0060 0.0102 0.9762 143.24 170.07
1.4600 0.0384 0.0057 0.0098 0.9626 129.16 157.71
1.4800 0.0387 0.0053 0.0094 0.9479 116.00 145.42
1.5000 0.0394 0.0047 0.0090 0.9323 103.84 133.54
1.5200 0.0401 0.0041 0.0086 0.9164 92.73 122.31
1.5400 0.0407 0.0037 0.0082 0.9004 82.71 111.89
1.5600 0.0411 0.0034 0.0078 0.8846 73.80 102.34
1.5800 0.0418 0.0031 0.0074 0.8693 66.02 93.72
1.6000 0.0427 0.0027 0.0071 0.8548 59.34 86.05
1.6200 0.0432 0.0022 0.0069 0.8417 53.73 79.36
1.6400 0.0437 0.0018 0.0067 0.8303 49.11 73.62
1.6600 0.0444 0.0013 0.0065 0.8207 45.39 68.81
1.6800 0.0452 0.0007 0.0063 0.8129 42.46 64.83
1.7000 0.0460 0.0003 0.0061 0.8066 40.20 61.61
1.7100 0.0464 0.0001 0.0061 0.8037 39.29 60.25
1.7200 0.0467 0.0000 0.0061 0.8010 38.50 59.04
1.7300 0.0469 0.0000 0.0061 0.7982 37.84 57.96
1.7400 0.0471 0.0000 0.0061 0.7951 37.27 57.01
1.7500 0.0470 0.0000 0.0061 0.7916 36.80 56.16
1.7600 0.0468 0.0010 0.0060 0.7871 36.40 55.39
1.7700 0.0465 0.0020 0.0060 0.7813 36.05 54.65
1.7800 0.0461 0.0030 0.0060 0.7734 35.73 53.90
1.7900 0.0453 0.0050 0.0060 0.7627 35.40 53.05
1.8000 0.0446 0.0070 0.0060 0.7479 35.00 52.00
1.8100 0.0430 0.0110 0.0060 0.7272 34.45 50.57
1.8200 0.0407 0.0170 0.0060 0.6980 33.66 48.54
1.8300 0.0389 0.0240 0.0060 0.6562 32.47 45.63
1.8400 0.0369 0.0360 0.0060 0.5942 30.62 41.29
1.8500 0.0286 0.0430 0.0060 0.4921 27.48 34.13
1.8600 0.0165 0.0500 0.0060 0.3035 20.20 20.77
1.8700 0.0000 0.0590 0.0060 0.0360 -8.49 19.78
Nach der Beschreibung der Skigeometrie können noch weitere Einträge folgen. Diese werden von uns, z.B. zur Berechnung der Biegesteifigkeit und der Torsionssteifigkeit verwendet. Hier folgen auch Daten, welche eine Bindungsplatte oder die Skibindung betreffen.
Man öffnet das Matlab-Programm und gibt z.B. den Befehl
druck ('ski', -1200, 20, 15, 0.01)
ein. Damit wird die Druckverteilung für den Ski, welcher in der Datei
ski.dat beschrieben ist, mit einer Normalbelastung von
Fz = -1200 N, einem Vorlagemoment von My = 20 Nm und einem
Kantmoment My = 15 Nm berechnet. In dieser Situation ist der Ski
mit 26 Grad aufgekantet. Die Schneehärteparameter d von 0.01 m
entspricht weichem Schnee. Die Ergebnisse der Berechnungen sind in
den Abb.
fig:d3a bis
fig:pca dargestellt.
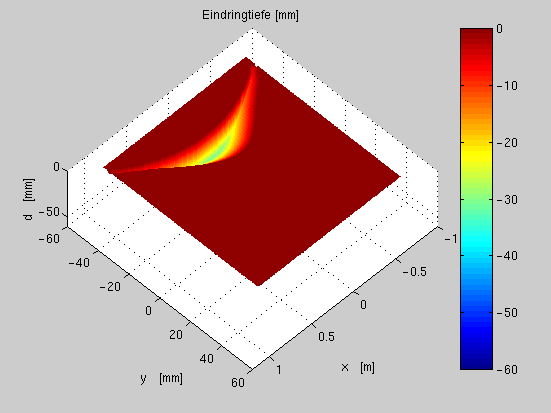
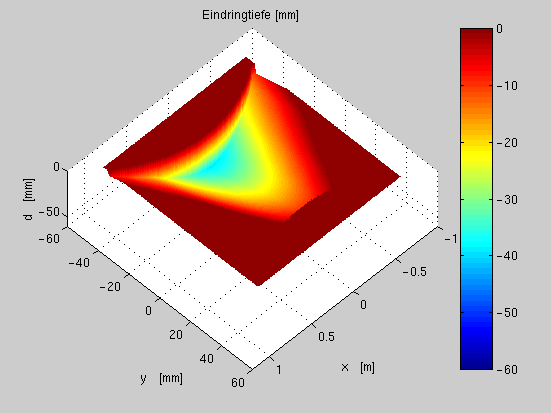
Abb.
fig:d3a zeigt die 3-D Ansicht der Eindringtiefe des Ski
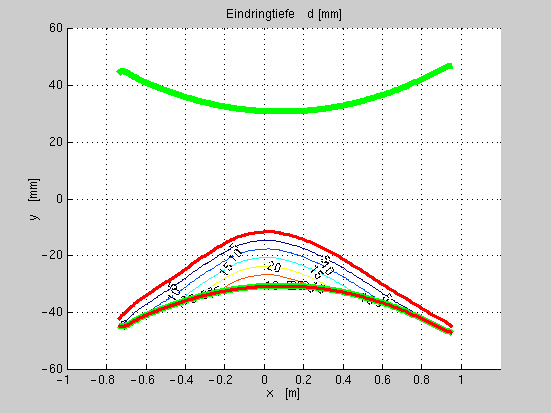
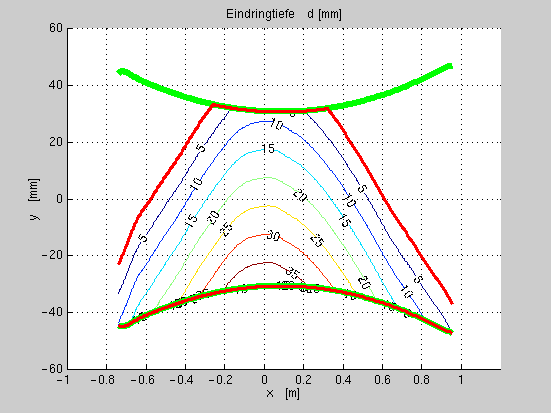
und Abb.
fig:dca stellt die Eindringtiefe als Konturplot dar.
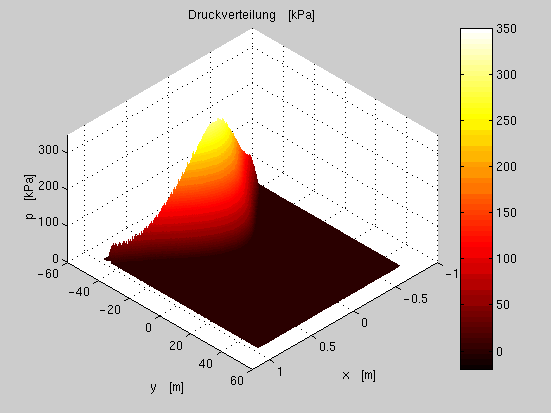
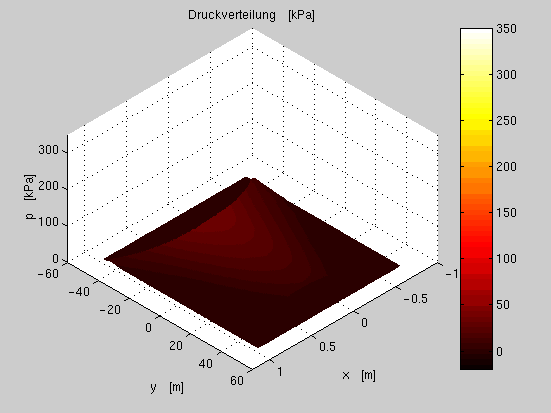
In Abb.
fig:p3a ist die 3-D Druckverteilung und in
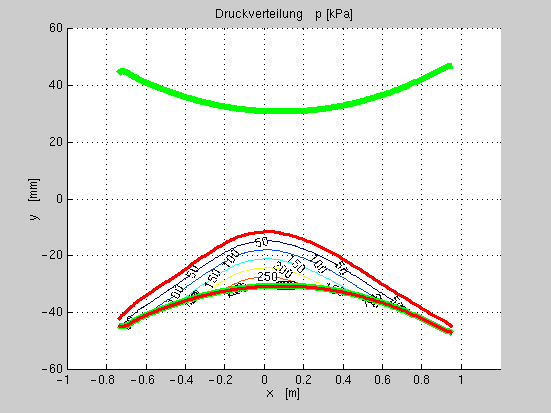
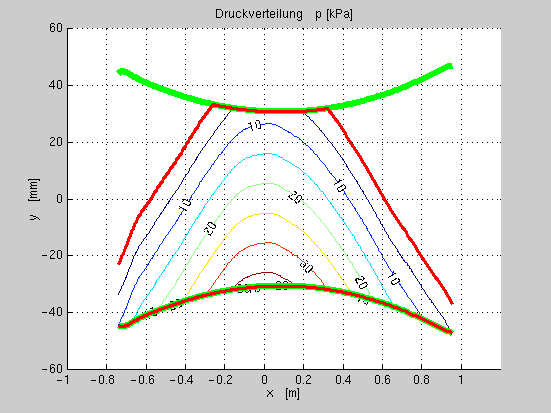
Abb.
fig:pca ein Niveaulinienplot der Druckverteilung
wiedergegeben.

Ein weiteres Beispiel ist mit
druck ('ski', -2000, 20, 55)
gegeben. In diesem Beispiel wird der Defaultwert d = 0.001 für
den Schneehärteparameter d verwendet.
Der Ski ist bereits mit 58 Grad aufgekantet.
Dementsprechend klein ist auch die Kontaktfläche des Ski mit der
Schneeoberfläche. Abb.
fig:d3b bis
fig:pcb
geben die Eindringtiefe und die Druckverteilung an.